Chemiestudent.de - Chemie Forum

Liebes Forum.

Ich muss bald eine Hausaufgabe an der Uni abgeben. Dabei bin ich leider auf eine Schwierigkeit gestoßen. Falls mir Jemand ein bisschen auf die Sprünge helfen könnte wäre das toll. Unter anderem habe ich schwierigkeiten mit dem differenzieren. Wenn ich zum Beispil eine Formel wie diese habe:



was bedeutet das f (ich denke die Frenkvenz) ganz unten rechts vor dem Gleichheitszeichen? Bis jetzt sehe ich, dass die differenzierte Länge durch die die differenzierte Temperatur etwas ergibt. Doch was das f da soll verstehe ich nicht.

Desweiteren muss ich von der genannten Formel auf diese Formel kommen:


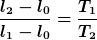
Die einzigen weiteren Informationen die ich bekomme sind:
und .

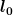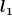Hierbei ist Länge wo der Draht nicht beeinflusst wurde. Die starttemperatur ist und die Startlänge . Danach wird die Temperatur und die Länge zu .

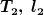Hoffentlich kann mir ja Jemand helfen? Verstehe nicht wie ich diese Aufgabe anpacken soll. Was mich insbesondere verwirrt sind die kleine Zeichen, welche an den Klammern angeheftet sind. Und das irritiert wenn die Aufgabe ansonsten fertig ist ^^

Vielen Dank im Voraus für Antworten! Bräuchte wirklich Hilfe hierbei!

Basilius hat geschrieben:


was bedeutet das f

Im Grunde ist f eine beliebige, differenzierbare Funktion zweier Variablen , die ich aus schreibtechnischen Gründen mit x und y bezeichne . Die "kleinen Zeichen, welche an den Klammern angeheftet sind" , bezeichnen die Größe, die beim Differenzieren als konstant angenommen wurde. :



Vereinfacht geschrieben :



Nun kann man sich vorstellen, dass x und y sich gerade so verändern, dass sich der Wert von f nicht ändert, die durch die Änderung von x und y bewirkten Veränderungen in Bezug auf f sich also gerade aufheben :